直线与平面的向量表示

二维平面中的直线表示

• 一般式：$Ax + By + C = 0$， 其中 $A, B$ 不能同时为 $0$ 。
• 斜截式：$y = kx + b$，其中 $k$ 是斜率，表示直线与 $x$ 轴正方向夹角的正切值，$b$ 是纵截距，表示直线与$y$ 轴交点的纵坐标。
• 点斜率：$y - y_1 = k(x - x_1)$，其中 $(x_1, y_1)$ 表示直线上一点，$k$ 表示直线斜率。
• 截距式：$\frac{x}{a} + \frac{y}{b} = 1$ ，其中 $a, b$ 分别表示直线与 $x$ 轴，$y$ 轴的截距，也就是与 $x$ 轴交点的横坐标，与 $y$ 轴交点的纵坐标。
• 两点式：$\frac{x-x_1}{x_2 - x_1} = \frac{y - y_1}{y_2 - y_1}$ ，其中 $(x_1, y_1), (x_2, y_2)$ 表示直线上两点的坐标。

直线与平面的向量表示

已知直线上点 $A$ 和直线的的方向向量 $\vec{b}$ ,根据向量的加法运算就可以把直线上任意一点 $R$ 都可以表示出来。

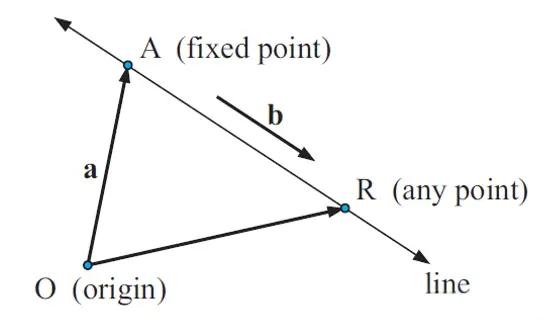
因为 $\vec{OR} = \vec{OA} + \vec{AR}, \vec{AR} = \lambda \vec{b}$，所以 $\vec{OR} = \vec{OA} + \lambda \vec{b}$。

这可以理解为，直线上任意一点都可以由直线上已知一点按照方向向量平移得到。根据上述原理，我们可以得到直线在二维，三维情况下的向量表示。

二维直线的向量表示

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + \lambda \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} $$

$$ \begin{cases} x &= x_0 + \lambda b_1 \\ y &= y_0 + \lambda b_2 \end{cases} $$

$$ \frac{x - x_0}{b_1} = \frac{y - y_0}{b_2} $$

三维直线向量表示

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + \lambda \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} $$

$$ \begin{cases} x &= x_0 + \lambda b_1 \\ y &= y_0 + \lambda b_2 \\ z &= z_0 + \lambda b_3 \end{cases} $$

$$ \frac{x - x_0}{b_1} = \frac{y - y_0}{b_2} = \frac{z - z_0}{b_3} $$

平面的向量表示

平面的向量表示有两种不同的方法：一种是利用向量的合成，一种是利用法向量。

向量的合成

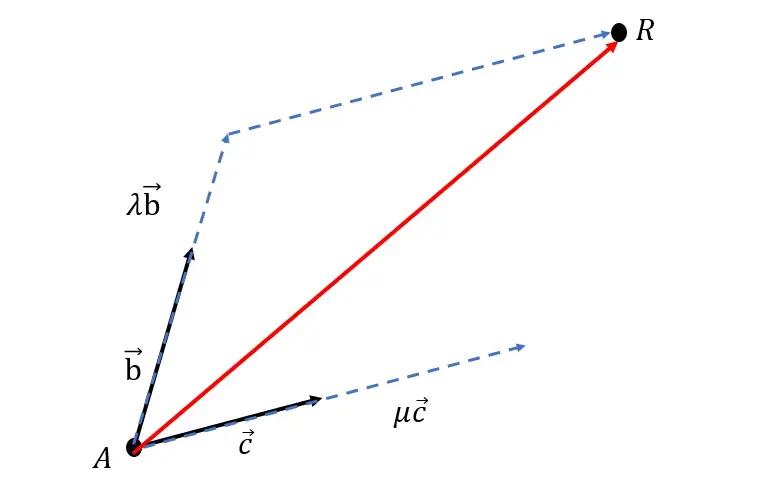
如果已知平面内一点 $A(a_1, a_2, a_3)$，和两个不平行的向量 $\vec{b} = \begin{pmatrix} b_2 \\ b_2 \\ b_3 \end{pmatrix}$ 和 $\vec{c} = \begin{pmatrix} c_1 \\ c_2 \\ c_3 \end{pmatrix}$，那么平面内任意一点 $R$ 都存在常数 $\lambda, \mu$ 使得以下等式成立：$\overrightarrow AR = \lambda \vec{b} + \mu\vec{c}$，又因为 $\overrightarrow OR - \overrightarrow OA = \lambda\vec{b} + \mu\vec{c}$，所以，$\overrightarrow OR = \overrightarrow OA + \lambda\vec{b} + \mu\vec{c}$，即：

$$ \begin{pmatrix} x \\ y \\z \end{pmatrix} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} + \lambda \begin{pmatrix}b_1 \\ b_2 \\ b_3 \end{pmatrix} + \mu \begin{pmatrix} c_1 \\ c_2 \\ c_3 \end{pmatrix} $$

法向量

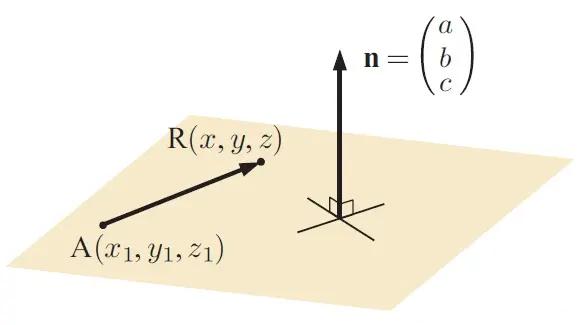
把与平面中任意向量都相互垂直的向量称为法向量。如果已知平面上一点 $A(x_1, y_1, z_1)$，和平面的法向量 $\vec{n} = \begin{pmatrix} a \\ b \\ c \end{pmatrix}$，那么点 $A$ 和平面内任意一点 $R(x, y, z)$ 所构成的向量 $\overrightarrow AR$ 与法向量垂直可得：$\vec{n} \cdot \overrightarrow AR = 0$，即

$\begin{pmatrix} a \\ b \\ c \end{pmatrix} \cdot \begin{pmatrix} x-x_1 \\ y-y_1 \\ z-z_1 \end{pmatrix} = 0$，即：$a(x-x_1) + b(y-y_1) + c(z-z_1) = 0$，最终得到平面的一般方程：$ax + by + cz = ax_1 + by_1 + cz_1$。因此，形如：$Ax + By + Cz = D$ 的都是平面方程，且 $\begin{pmatrix} A \\ B \\ C \end{pmatrix}$ 是该平面的法向量。

例如：一平面方程 $2x + 4y + z = 1$，那么该平面的法向量为 $\begin{pmatrix} 2 \\ 4 \\ 1 \end{pmatrix}$ 。$3x + 5y = 1$ 的法向量为 $\begin{pmatrix} 3 \\ 5 \\ 0\end{pmatrix}$。