游戏开发中的数学：点到直线与平面距离的数学推导与实现

点到直线的距离公式

任意一条直线：$ax + by + c = 0$，$A(x_0, y_0)$ ，求点$A$ 到直线的距离？

求一个向量在另一向量方向上投影的长度，可以推出如下结果：

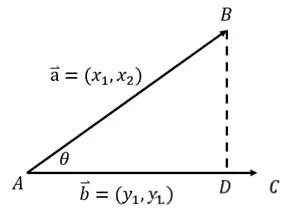
$$ |AD| = |AB|cos \theta = |\overrightarrow AB| \cdot \begin{vmatrix} \frac{\overrightarrow AB \cdot \overrightarrow AC}{|\overrightarrow AB| \cdot |\overrightarrow AC|} \end{vmatrix} = \begin{vmatrix} \overrightarrow AB \cdot \frac{\overrightarrow AC}{|\overrightarrow AC|} \end{vmatrix} $$

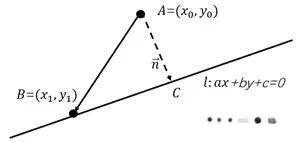
根据投影的计算公式可得，$|\overrightarrow AB \cdot \frac{\vec{n}}{|\vec{n}|}| =|(x_1 - x_0, y_1 - y_0) \cdot \frac{(a, b)}{\sqrt{a^2 + b^2}}| = \frac{1}{\sqrt{a^2 + b^2}} |a(x_1 - x_0) + b(y_1 - y_0)| = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}}$

任意一点 $A(x_0, y_0)$ 到直线 $ax + by + c = 0$ 的距离公式可以记作：

$$ |AC| = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}} $$

点到面的距离公式

求点$A(x_0, y_0, z_0)$ 到平面 $\pi：ax + by + cz + d = 0$ 的距离。

与点到直线的距离做法类似，先在平面 $\pi$ 上找一点 $B(x_1, y_1, z_1)$，根据平面方程有：$ax_1 + by_1 + cz_1 - d = 0$，平面 $\pi$ 的法向量 $n = (a, b, c)$。

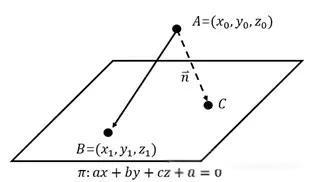
$|AC| = |\overrightarrow AB \cdot \frac{\vec{n}}{|\vec{n}|}|$ 可以进一步推导出：

点 $A(x_0, y_0, z_0)$ 到平面 $\pi：ax + by +cz + d = 0$ 的距离：

$$ |AC| = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2+b^2+c^2}} $$

n 维空间中，点 A 到 n 维超平面的距离

$A(x_0, x_1, x_2, ... , x_n)$，超平面 $\pi$ ：$a_0y_0 + a_1y_1 + a_2y_2 + \cdots + a_ny_n + d = 0$，则点 $A$ 到 $n$ 维超平面 $\pi$ 的距离为：

$$ |AC| = \frac{|a_0x_0 + a_1x_1 + a_2x_2 + \cdots + a_nx_n + d|}{\sqrt{a_0^2 + a_1^2 + \cdots + a_n^2}} $$